If it wasn't for spam, I'd get hardly any comments at all. As with many things in life, spam is simultaneously interesting and frustrating. The interesting part is trying to decipher messages prepared by either computers or by people possessing only a passing familiarity with the English language. The frustrating part is, well, it's spam. By sheer volume, my most frequent spammer advertises a web site about binary options. Clicking on that link, or going to that web site, is not on my agenda. However, my curiosity has been stoked. What exactly is a binary option? The Oracle Google was consulted. Wiki here. Fun cut-and-paste excerpt, that makes perfect sense to me, is here:
A binary call option is, at long expirations, similar to a tight call spread using two vanilla options. One can model the value of a binary cash-or-nothing option, C, at strike K, as an infinitessimally tight spread, where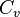 
is a vanilla European call:[page needed],
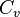is a vanilla European call:[page needed],
Thus, the value of a binary call is the negative of the derivative of the price of a vanilla call with respect to strike price:
When one takes volatility skew into account,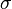 
is a function of 
:
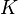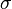is a function of :
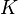The first term is equal to the premium of the binary option ignoring skew:
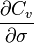is the Vega of the vanilla call; 
is sometimes called the "skew slope" or just "skew". Skew is typically negative, so the value of a binary call is higher when taking skew into account.
Posts
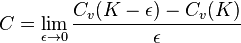
No comments:
Post a Comment